10.06.2024 | Michael Veser
Wie Daten zur Nutzung mit AI-Modellen gespeichert werden
Dieser Artikel erläutert technische Grundlagen von generativen AI Systemen. Er dient dem besseren Verständnis unserer Artikel zu Security Fragestellungen rund um den Einsatz von AI Systemen.
In der Welt der Künstlichen Intelligenz spielen Large Language Models (LLMs) eine zunehmend zentrale Rolle bei der Verarbeitung und Analyse menschlicher Sprache. Um diese komplexen Modelle effizient mit eigenen Daten zu nutzen, müssen grosse Mengen von Textdaten in eine Form umgewandelt werden, die von AI-Modellen verarbeitet werden kann. Dieser Prozess umfasst zwei entscheidende Schritte: die Tokenisierung und die Einbettung (Embedding). In diesem Artikel untersuchen wir, wie diese Techniken verwendet werden, um Daten für die Nutzung durch LLMs vorzubereiten und zu speichern. Ich werde die technischen Mechanismen dieser Prozesse erläutern, ihre Bedeutung im Kontext der maschinellen Sprachverarbeitung verdeutlichen und aufzeigen, wie sie die Grundlage für die fortgeschrittenen Fähigkeiten moderner Sprachmodelle bilden. Durch das Verständnis dieser fundamentalen Technologien können wir besser nachvollziehen, wie LLMs komplexe Analyseaufgaben bewältigen und tiefere Einblicke in die zugrunde liegende Technik gewinnen. Anhand eines typischen Anwendungsfalls, der Analyse von Logdaten, werden wir die Schritte genauer betrachten.
Klassischer Ansatz: Parsing
Bei der Analyse von Logfiles spielt das Parsing unstrukturierter Daten eine zentrale Rolle. Dieser Prozess transformiert den eingehenden Datenstrom in eine strukturierte Form, indem er reguläre Ausdrücke, Formaterkennung und teilweise auch maschinelles Lernen nutzt. Dabei werden spezifische Informationen wie Zeitstempel, IP-Adressen und Servernamen aus den Daten extrahiert. Sobald die Daten strukturiert sind, lassen sich weitere Analysen wie Häufigkeitsauswertungen, das Erkennen von Anomalien und die Sortierung nach spezifischen Parametern effizient durchführen.
Einer der grössten Vorteile dieses Ansatzes liegt in der leistungsstarken Suchfunktion, die es ermöglicht, schnell auf bestimmte bekannte Parameter zuzugreifen. Allerdings gibt es auch Herausforderungen: Der anfängliche Aufwand für das Einrichten des Parsingsystems ist oft erheblich. Zudem sind die Möglichkeiten begrenzt, Ähnlichkeiten zwischen verschiedenen Datensätzen zu erkennen. Das liegt daran, dass das Parsing primär darauf ausgerichtet ist, explizite Informationen zu identifizieren und weniger darauf, versteckte Muster oder Beziehungen zwischen Datenpunkten zu analysieren. Durch Varianzen der Eingangsdaten kann zudem die Fehleranfälligkeit schnell zu einem einschränkenden Faktor werden.
Tokenisierung: Der Umgang mit unstrukturierten Informationen
Im Gegensatz zum Parsing, das sich auf das Erkennen spezifischer Inhalte in konsistenter Form konzentriert, teilt die Tokenisierung den Eingangstext ohne Berücksichtigung des konkreten Inhalts in kleinere Einheiten auf – sogenannte Token. Dieser Prozess kann auf verschiedene Arten erfolgen: Einige Ansätze verwenden vordefinierte Längen, um den Text zu segmentieren, während andere auf Trennzeichen wie Leerzeichen oder Satzzeichen basieren, um natürliche Grenzen innerhalb des Textes zu identifizieren.
Darüber hinaus gibt es Methoden, die den Text in grössere Abschnitte oder «Chunks» zerlegen. Diese Chunks können ganze Sätze oder Satzteile umfassen und dienen dazu, den Text in logisch zusammenhängende Einheiten zu unterteilen, die dann weiter analysiert werden können.
Im nächsten Schritt werden wir die verschiedenen Tokenisierungsansätze genauer betrachten und sowohl ihre Vorteile als auch ihre Nachteile detailliert erörtern. Dieser Überblick ermöglicht es, ein tieferes Verständnis dafür zu entwickeln, wie diese Methoden die Textanalyse beeinflussen und welche Techniken für spezifische Anwendungen am besten geeignet sind.
Interpunktion-basierte Tokenisierung
Bei der auf Satzzeichen basierenden Tokenisierung teilt das Verfahren den Text normalerweise nicht in Token fester Länge auf, obwohl es eine vordefinierte maximale Länge geben kann. Diese Art der Tokenisierung trennt vielmehr die Textsequenz an jedem Satz- oder Leerzeichen, was in der Regel zu kurzen Token führt. Ein spezielles Submodell dieser Methode ist die «Whole sentence tokenization», bei der ein ganzer Satz als einzelner Token behandelt wird. Dies ermöglicht die Verarbeitung des Textes in grösseren, zusammenhängenden Einheiten, die den Kontext besser bewahren können.
Leerzeichen-basierte Tokenisierung
Bei der «Whitespace tokenization» nutzt das Verfahren Leerzeichen als Trennzeichen, um den Text in einzelne Token zu unterteilen. Diese Methode führt bei der Analyse von Logfiles zu einem Ergebnis, das den durch Parsing-Methoden erzeugten Strukturen stark ähnelt. Indem Leerzeichen als klare Abgrenzung zwischen den Token verwendet werden, lässt sich der Text effektiv in diskrete, leicht handhabbare Einheiten aufteilen. Diese Art der Tokenisierung ist besonders nützlich, um klare, durch Leerzeichen getrennte Daten wie Logeinträge zu verarbeiten.
Tokenisierung anhand fester Längendefinition
Bei der Tokenisierung anhand fester Länge wird der Text unabhängig von Leerzeichen oder Satzzeichen in gleich grosse Token zerlegt. Diese Methode unterteilt die Textsequenz systematisch in Einheiten einer spezifischen Länge, ohne dabei die natürlichen Sprachgrenzen wie Wörter oder Sätze zu berücksichtigen. Diese Art der Tokenisierung kann besonders in Szenarien nützlich sein, in denen eine gleichmässige Verarbeitung der Daten gewünscht ist und die Position jedes Zeichens im Text von Bedeutung sein könnte.
Fazit
Der Informationsgehalt der Daten kann stark von der gewählten Tokenisierungsmethode abhängen. Insbesondere bei der Einbettung der Token können sowohl zu kurze als auch zu lange Token zu einem Informationsverlust führen. Es ist daher entscheidend, die Tokenisierungsmethode sorgfältig zu wählen, um sicherzustellen, dass die relevanten Datenmerkmale effektiv erfasst und erhalten bleiben.
Einbettung in den Vektorraum
Im Anschluss an die Zerlegung des Eingangsdatenstroms wird jedem Token eine eindeutige Vokabular-ID zugewiesen. Diese IDs dienen als numerische Repräsentanten der Token, die jeweils ein Wort, ein Satzzeichen oder eine andere sprachliche Einheit repräsentieren. Das zugrunde liegende Vokabular, das während des Vortrainings des Modells entwickelt wird, umfasst typischerweise eine umfangreiche Palette von Einträgen, die die erkannten Wörter und Symbole abbilden.
Die Zuweisung dieser Vokabular-IDs standardisiert und vereinfacht die Verarbeitung von Textdaten erheblich. Indem jeder Token auf eine Zahl reduziert wird, können die Modelle unabhängig von der ursprünglichen Sprache oder Formatierung der Texte arbeiten, was den Verarbeitungsprozess beschleunigt und den Speicherbedarf senkt. Darüber hinaus ermöglichen diese numerischen Repräsentationen es dem Modell, Beziehungen zwischen den Daten zu erkennen und maschinelle Lernprozesse effizienter zu gestalten. Solche Prozesse stützen sich stark auf numerische Operationen und die klare numerische Zuordnung durch Vokabular-IDs erleichtert die Integration sprachlicher Informationen in mathematische Modelle.
Einmal mit einer ID versehen, können die Token in die nächste Phase der Sprachverarbeitung übergehen: das Embedding. In dieser Phase werden die Token, die nun als numerische IDs vorliegen, in vieldimensionale Vektoren umgewandelt. Diese Vektoren, auch Embeddings genannt, repräsentieren die semantischen und syntaktischen Eigenschaften der Token in einem kontinuierlichen Vektorraum. Sie ermöglichen es dem Modell, tiefgreifende linguistische Muster zu erkennen und zu lernen, was die Grundlage für komplexe Aufgaben wie Übersetzungen, Textzusammenfassungen und die Beantwortung von Fragen bildet.
Die Funktionsweise von Einbettungsmodellen
Einbettungsmodelle sind entscheidend dafür, Inhalte effektiv in einem mehrdimensionalen Vektorraum einzubetten, indem sie die semantischen und syntaktischen Eigenschaften von Textdaten in numerische Vektoren umwandeln. Diese Modelle analysieren den Kontext, in dem Wörter und Phrasen auftreten, einschliesslich ihrer Häufigkeit und den Beziehungen zu anderen Wörtern im Text. Durch diese Analyse erzeugen Einbettungsmodelle dichte Vektordarstellungen, die dann im Vektorraum so positioniert werden, dass ähnliche oder zusammenhängende Begriffe nahe beieinander liegen. Dies ermöglicht es, die semantische Nähe zwischen unterschiedlichen Wörtern oder Phrasen zu messen und abzubilden. Neben der Lage im Vektorraum spielt auch die «Blickrichtung» innerhalb des Raumes eine grosse Rolle. So würde beispielsweise der Begriff «Mutter» in Relation zu «Vater» in einer ähnlichen Blickrichtung liegen wie «Frau» zu «Mann».
Ein weiterer wichtiger Aspekt von Einbettungsmodellen ist ihre Fähigkeit, durch Feintuning angepasst zu werden. Dies bedeutet, dass ein bereits vortrainiertes Modell weiterhin mit spezifischeren Daten trainiert werden kann, um die Genauigkeit der Einbettung zu erhöhen, besonders wenn es um spezialisierte Terminologie oder bestimmte sprachliche Kontexte geht. Feintuning ermöglicht eine feinere Abstimmung der Modelle auf die spezifischen Anforderungen und Bedürfnisse, wodurch die Effektivität des Modells in spezialisierten Anwendungen verbessert werden kann.
Diese Fähigkeit, Text in präzise, kontextuell relevante Vektoren zu übersetzen, macht Einbettungsmodelle zu einem mächtigen Werkzeug in der Welt der maschinellen Sprachverarbeitung. Sie erlauben es uns, tiefere und nuanciertere Einblicke in die Bedeutungen, die hinter Wörtern und ihren Beziehungen stehen, zu gewinnen und leisten somit einen unverzichtbaren Beitrag zur Entwicklung intelligenter, kontextbewusster Systeme. Diese Funktionalität legt den Grundstein für die Ähnlichkeitssuche.
Ähnlichkeitssuche
Nachdem wir die Tokenisierung und das Einbetten von Daten in einem mehrdimensionalen Raum verstanden haben, können wir uns der Frage widmen, wie diese eingebetteten Daten genutzt werden können, um beispielsweise Ähnlichkeiten zwischen verschiedenen Logeinträgen zu identifizieren. Hier kommen Algorithmen wie die Kosinus-Ähnlichkeit und k-nächste Nachbarn (kNN) ins Spiel.
Die Kosinus-Ähnlichkeit misst den Kosinus des Winkels zwischen zwei Vektoren im Vektorraum. Diese Metrik ist besonders nützlich, da sie unabhängig von der Grösse der Vektoren ist, was bedeutet, dass nur die Richtung der Vektoren und nicht ihre Länge berücksichtigt wird. Der Wertebereich dieser Metrik liegt zwischen -1 und 1, wobei 1 eine perfekte Übereinstimmung (gleiche Orientierung), 0 keine Korrelation und -1 genau entgegengesetzte Richtungen anzeigt. Die Vorteile der Kosinus-Ähnlichkeit liegen in ihrer geringen Komplexität und schnellen Implementierung, was sie ideal für Systeme macht, die schnelle Ähnlichkeitssuchen durchführen müssen. Allerdings ist es wichtig, geeignete Schwellenwerte für die Ähnlichkeitssuche festzulegen, um eine optimale Balance zwischen der Einbeziehung irrelevanter Ergebnisse und dem Übersehen wichtiger Ergebnisse zu finden.
Als Alternative oder Ergänzung zur Kosinus-Ähnlichkeit bietet der Algorithmus k-nächste Nachbarn (kNN) eine Methode, bei der die Klassifizierung von Datenpunkten auf der Basis der nächsten, bereits klassifizierten Punkte in ihrem Umkreis erfolgt. kNN ist ein intuitiver Ansatz: Ein neuer Punkt wird den Klassen seiner nächsten Nachbarn zugeordnet, wobei «k» die Anzahl der zu berücksichtigenden Nachbarn angibt. Bei einem k von 1 wird der Punkt einfach der Klasse seines nächsten Nachbarn zugewiesen. Bei einem grösseren k werden die häufigsten Klassen innerhalb der nächsten k-Punkte berücksichtigt. Es empfiehlt sich, eine ungerade Zahl für k zu wählen, um bei der Klassenzuweisung eine klare Mehrheit zu haben. Ein Hauptnachteil von kNN ist jedoch seine Skalierbarkeit, besonders bei grossen Datensätzen, da die Entfernung zu allen anderen Punkten vorberechnet werden muss. Um die Herausforderungen der Hardwareeffizienz zu bewältigen, existieren angepasste Versionen wie «Approximate nearest neighbor», die eine schnellere, wenn auch etwas weniger genaue Nachbarschaftssuche ermöglichen.
Zusammengefasst bieten sowohl Kosinus-Ähnlichkeit als auch kNN leistungsfähige Werkzeuge für die Ähnlichkeitssuche in eingebetteten Daten. Während Kosinus-Ähnlichkeit sich durch geringe Komplexität und schnelle Ausführung auszeichnet, bietet kNN eine intuitive, wenn auch potenziell rechenintensive Methode zur Datenklassifizierung, die besonders bei kleineren Datensätzen oder in angepassten Implementierungen effektiv ist. Beide Methoden sind entscheidend für Aufgaben wie die Anomalieerkennung und das Retrieval von relevanten Suchergebnissen, indem sie es ermöglichen, die Beziehungen zwischen Datenpunkten präzise zu bestimmen.
Test mit Logfiles
Um die ganze Theorie nun mit einem konkreten Beispiel zu testen, betten wir drei Zeilen eines Logfiles in einen vereinfachten dreidimensionalen Vektorraum ein:
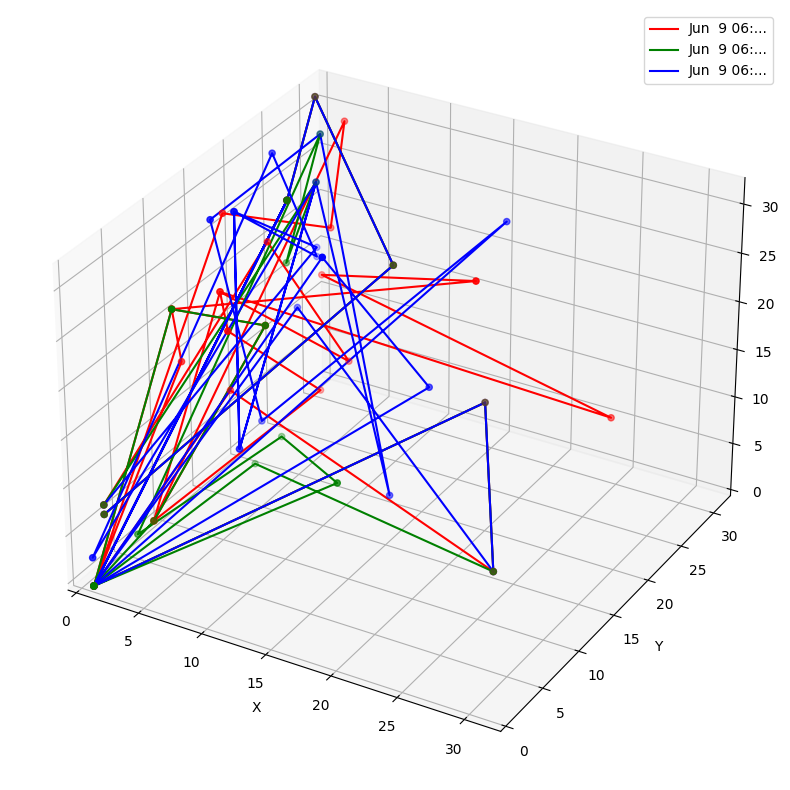
Fazit
In diesem Artikel haben wir die entscheidenden Prozesse der Tokenisierung und Einbettung (Embedding) untersucht, die notwendig sind, um Textdaten für den Einsatz in Large Language Models (LLMs) aufzubereiten. Wir haben gesehen, wie durch verschiedene Methoden der Tokenisierung Texte in kleinere, handhabbare Einheiten zerlegt werden, die dann durch Einbettungsmodelle in einem mehrdimensionalen Vektorraum repräsentiert werden. Die Fähigkeit dieser Modelle, die semantischen und syntaktischen Eigenschaften der Sprache zu erfassen und in numerische Form zu bringen, ist grundlegend für weiterführende Aufgaben.
Zudem haben wir uns die Bedeutung von Ähnlichkeitssuchen mithilfe von Algorithmen wie der Kosinus-Ähnlichkeit und k-nächsten Nachbarn (kNN) angesehen, welche es ermöglichen, Beziehungen zwischen eingebetteten Daten zu erkennen und zu nutzen, etwa für die Klassifizierung oder Anomalieerkennung.
Durch die Anpassung dieser Modelle mittels Feintuning können die Embeddings weiter verfeinert werden, um spezifische Anforderungen und Kontexte besser zu berücksichtigen, was in einem der späteren Artikel noch wichtig werden wird.
